What Values of a and B Will Make the Function F Continuous

Find values of $a$ and $b$ that make the function continuous everywhere.

Solution 1

I've seen this problem before and it looks like this may be the function you are trying to make continuous here:

$f(x) = \begin{cases} \frac{x^2-4}{x-2} & \mbox{if } x<2 \\ ax^2-bx+1 & \mbox{if } 2\leq x<3 \\ 4x-a+b & \mbox{if } x\geq 3 \end{cases}$

To make sure $f$ is continuous at $x=2$ you want to use the definition of what it means to be continuous by solving $\lim_{x \to 2} f(x) = f(2).$ Since $f$ is different from the left and right side of $x=2$, you need to instead find each one sided limit.

$$\lim_{x \to 2^{-}} f(x) = f(2)$$

$$\lim_{x \to 2^{+}} f(x) = f(2).$$

First the left sided limit: $$\lim_{x \to 2^{-}} \frac{x^2-4}{x-2} = f(2)$$ $$\lim_{x \to 2^{-}} \frac{(x+2)(x-2)}{x-2} = f(2)$$ $$\lim_{x \to 2^{-}} (x+2) = f(2)$$ $$4=f(2)$$ $$4=a(2)^2-b(2)+1$$ $$4=4a-2b+1$$ $$3=4a-2b$$ If you do this with the right sided limit, you'll see that you end up with $4a-2b+1=4a-2b+1$, which doesn't really give you any useful information. Now you want to do the same thing to make sure $f$ is continuous at $x=3$ $$\lim_{x \to 3^{-}} f(x) = f(3)$$ $$\lim_{x \to 3^{-}} ax^2-bx+1 = 12-a+b$$ $$a(3)^2-b(3)+1 = 12-a+b$$ $$9a-3b+1 = 12-a+b$$ $$10a-4b=11$$

And in this case, the right sided limit won't contribute anything useful. Now you just need to solve the following system of equations:

$$3=4a-2b$$ $$10a-4b=11$$

Here's a link to a very detailed work-through of a very similar problem with a bit more explanation of why this works.

https://jakesmathlessons.com/limits/solution-find-the-values-of-a-and-b-that-make-f-continuous-everywhere/

Solution 2

If $f$ is continuous then :

$f(2)=\underset{x\rightarrow2}{\lim}f(x)=2^2-\frac{4}2-2=a(2^2)-b(2)+1$

Therefore $4a-2b+1=4-2-2=0$ hence $4a-2b+1=0$.

Same reasoning around $x=3$ :

$a(3^2)-b(3)+1=4(3)-a+b$ (ie) $9a+3b+1=12-a+b$ therefore $10a-4b=11$

You just need to solve $\begin{cases}4a-2b=-1\\10a-4b=11\end{cases}$ to find $a$ and $b$.

Solution 3

For continuity at 2, we need $\lim_{x\to2^{+}}f(x)=f(2)$ and $\lim_{x\to2^{-}}f(x)=f(2)$, so $4a-2b+1=4a-2b+1$ and $4-2-2=4a-2b+1$, so $4a-2b=-1$.

For continuity at 3, we need $\lim_{x\to3^{+}}f(x)=f(3)$ and $\lim_{x\to3^{-}}f(x)=f(3)$, so $12-a+b=9a-3b+1$ and $9a-3b+1=9a-3b+1$, so $10a-4b=11$.

Now solve these two equations for a and b.

(I am assuming the last part of the definition should say for $x>3$.)

Comments

I need some help with this question:

Find the values of $a$ and $b$ that make $f$ continuous everywhere.

$$f(x)=\begin{cases} x^2 − 4/x-2, &\text{if }x < 2\\ ax^2-bx+1, &\text{if } 2 ≤ x ≤ 3\\ 4x - a + b, &\text{if } x ≥ 3\end{cases}$$

I started by writing two expressions for $a$ and $b$ based upon the left and right limits of each piece's endpoints. But I ended up with $a=3/2$ and $b=2/3$. Where did I go wrong?
- What equations did you get for a and b after you found the one-sided limits?
- All I did was plug in numbers into the equation at x = 2 (for x^2-4/x-2 and ax^2-bx+1) and then x = 3 (ax^2-bx+3 and 4x-a+b)
- @Michael are you sure it's $4/x$ and not $4x$ for the part where $x<2$ ?
- Maybe the first option was meant to evaluate to $(x^2-4)/(x-2)$? The original was somewhat unclear on this matter. (Also, both the second and third options seem to apply when $x=3$, which won't change the answer, but you should probably check if the second option is meant to hold when $... x < 3$ or the third option when $x > 3$.)
so A = 7/5 and B = -33/10?
Ugh! It didn't like either of those answers I wrote...
@Michael Maybe $a=2,b=\frac{-9}2$ ?
Nope, that's not the answer either...
@Michael What is it supposed to be ?
No idea... It doesn't show the answer...
@Michael Here fixed
@Michael $a=13/2,b=27/2$ ?
Mmmm Still incorrect... I think B is supposed to cancel out...
@Michael Can you link me to the source ? Both answers that have been posted here give the $a,b$ I just posted above, so ...
I'm afraid there isn't a source... I ran out of attempts anyways... It still didn't show me the correct answer...
It was just a homework question on a math assignment...
@Michael Look at this prntscr.com/4lxjou to me it IS continuous (I drew it in red). Maybe the form you answered on didn't support fractions, or something like that.

Recents

johnsonlibing1980.blogspot.com

Source: https://9to5science.com/find-values-of-a-and-b-that-make-the-function-continuous-everywhere

What Values of a and B Will Make the Function F Continuous

Find values of $a$ and $b$ that make the function continuous everywhere.

Solution 1

Solution 2

Solution 3

Related videos on Youtube

Comments

Recents

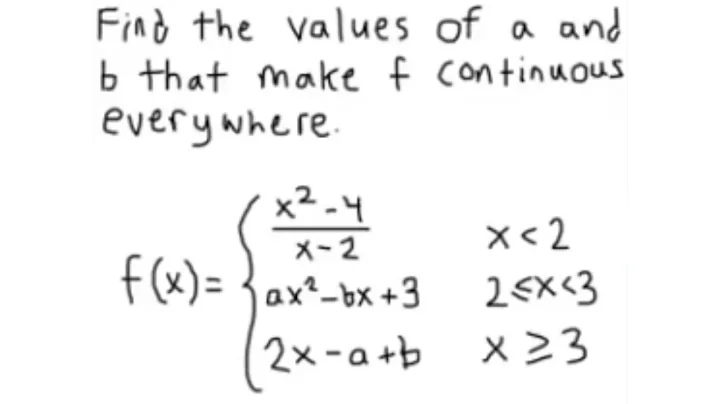
0 Response to "What Values of a and B Will Make the Function F Continuous"

Post a Comment

Iklan Atas Artikel

Iklan Tengah Artikel 1

Iklan Tengah Artikel 2

Iklan Bawah Artikel